


The Excel template developed by Hoyle and Henley generates other parameters that can be used in probabilistic sensitivity analysis like the Cholesky decomposition matrix, which will be discuss in a later blog. Moreover, we can take advantage of the Weibull distribution to extrapolate the survival probability over the cohort’s lifetime giving us the ability to model lifetime horizons. Using the Hoyle and Henley’s Excel template to generate the survival probabilities, which are then used in an R script to generate the lambda and gamma parameters, provides a powerful tool to integrate Weibull parameters into a Markov model. Using the Kaplan-Meier curves from published sources can help you to generate your own time-varying survival curves for use in a Markov model. Using existing studies as a reference will allow you to make adjustments to your survival curves that will give them credibility and validation to your cost-effectiveness analysis. Moreover, if you want to compare your simulated cohort’s survival performance to a reference specific to your chronic disease cohort, you can search the literature for previously published registry data or epidemiology studies. National Center for Health Statistics has life tables that you can use to estimate the life expectancy of the general population, which you can compare to your simulated cohort.
However, it is always good practice to calibrate your survival curves with the most recent data on the population of interest. This method is very useful when simulating chronic diseases.
#Engauge digitizer curve point tool how to
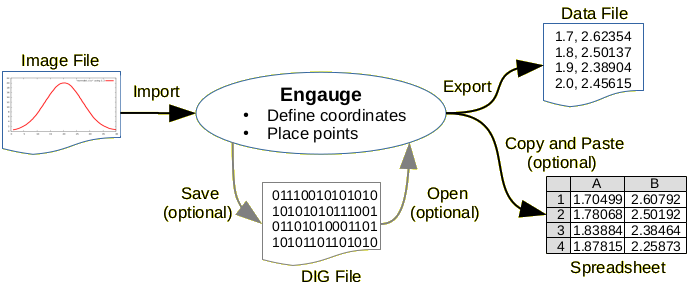
We will use a three-state Markov model to illustrate how to incorporate the Weibull parameters and generate a survival curve ( Figure 1).Īfter extrapolating the survival curve beyond the reference Kaplan-Meier curve limit of 40 months, you can estimate the lifetime horizon for a cohort of patients using a Markov model. Link to the Markov model used in this tutorial can be found here. Finally, we’ll show how to extrapolate the survival curve to go beyond the time frame of the Kaplan-Meier curve so that you can perform cost-effectiveness analysis across a lifetime horizon.ĭescribe how to incorporate the Weibull parameters into a Markov modelĬompare the survival probability of the Markov model to the reference Kaplan-Meier curve to validate the method and catch any errorsĮxtrapolate the survival curve across a lifetime horizon In the second part of this tutorial, we will take you through the process of incorporating these Weibull parameters to simulate survival using a simple three-state Markov model. The Weibull parameters will allow you to generate survival curves for cost-effectiveness analysis. However, you do have a map.In a previous blog, we provided instructions on how to generate the Weibull curve parameters (λ and γ) from an existing Kaplan-Meier curve. You ride a bike or boat and want to know how much distance you covered in your last trip, but you do not have an odometer or GPS unit. You are a webmaster with visitor statistics charts and you want to do statistical analyses. You are a graduate student gathering historical data from charts for your thesis. You are an engineer with some graphs in decades-old documents, but you really need the numbers represented in those graphs so you can do analyses that will determine if a space vehicle is safe to fly. The term "Engauge" in Engauge Digitizer was invented for this project, since there seems to be no similar term in common use. You add three axis points to define the axes, then other points along your curve(s).The final result is digitized data that can be used by other tools such as Microsoft Excel and Gnumeric.Įngauge (from en "make" and gauge "to measure") verb meaning to convert an image file containing a graph or map, into numbers. The process starts with an image file containing a graph or map. The numbers can be read on the screen, and written or copied to a spreadsheet. The image file can come from a scanner, digital camera or screenshot.
#Engauge digitizer curve point tool software
This open source, digitizing software converts an image file showing a graph or map, into numbers.


 0 kommentar(er)
0 kommentar(er)
